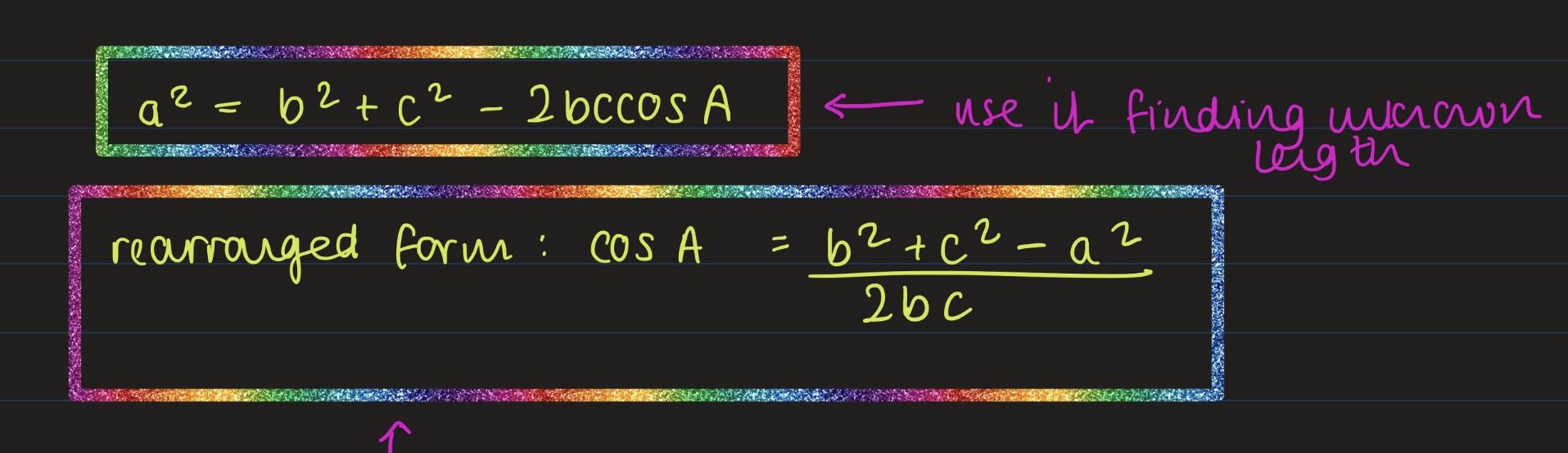Integration
Indefinite Integration
- Know and be able to use the fundamental theorem of calculus
- Understand and be able to use the terms indefinite and definite when applied to integrals
- Be able to integrate xn (except n = -1) and related sums, differences and multiples
- Solve problems including evaluating a constant of integration
Definite Integration and Complex Functions
- Be able to integrate ekx,1⁄x, sin kx, cos kx, and related sums, differences and constant multiples
- Integrals of arcsin, arccos and arctan will be given if required
- This includes using trigonmetric relations (eg double angle formulae) to integrate functions such as cos2x
- Be able to evaluate definite integrals
- Be able to use a definite integral to find the area between a curve and x-axis
Vectors
Vectors in 2D
- Be able to use vectors in two dimensions
- Column vectors and i,j notation
- Difference between a scalar and vector and distinguish between them when writing
- Calculate magnitude and direction of a vector
- Convert between magnitude/direction form and component form
- Calculate the modulus of a vector and interpret as magnitude
- Be able to add vectors diagrammatically
- Perform vector addition
- Multiply vectors by scalars
- Understand and be able to use position vectors
- Understand the meaning of displacement vector, component vector, resultant vector, parallel vector, equal vector and unit vector
- Calculate the distance between two points represented by position vectors
- Use vectors to solve problems in pure mathematics and in context, including forces (see forces notes)
- Use vectors to solve problems in kinematics (see kinematics notes)
Vectors in 3D
- Be able to use vectors in three dimensions
- Column vectors and i,j notation
- Extend points above to 3D (excluding the direction of a 3D vector)
Modelling in Mechanics
- Understand and be able to use the fundamental quantities and units in the S.I. system.
- Understand that the three base quantities of length, time and mass are mutually independent.
- Understand and be able to use derived quantities and units.
- Be able to add the appropriate unit to a given quantity.
Kinematics
Summary
Introduction
- Understand and be able to use the language of kinematics: position, displacement, distance, distance travelled, velocity, acceleration, equation of motion.
- Understand the vector nature of dispalacement, velocity and acceleration and the scalar nature of distance travelled and speed.
Graphical Representation
- Understand, use and interpret graphs in kinematics for motion in a straight line.
- Be able to interpret displacement-time and velocity-time graphs.
- Use the interpretations of gradients and areas of these graphs as necessary.
Non-Uniform Acceleration (Calculus)
- Be able to use differentiation and integration with respect to time in 1D to solve simple problems.
Non-Uniform Acceleration (Calculus) and Vectors
- Be able to extend the application of differentiation and integration to two dimensions using vectors.
- Questions set may involve either column vector or i,j notation.
Constant Acceleration
- Understand, use and derive the formulae for constant acceleration for motion in a straight line.
- Be able to derive the formulae by integration/differentiation, using and interpreting graphs and substitution.
Constant Acceleration and Vectors
- Extend the constant acceleration formulae to motion in 2D using vectors.
- Questions set may involve either column vector or i,j notation.
Motion Under Gravity
- Be able to model motion under gravity in a vertical plane using vectors where a = -gj.
Projectiles
- Be able to model the motion of a projectile as a particle moving with constant acceleration and understand the limitation of this model.
- Use horizontal and vertical equations of motion to solve problems on the motion of projectiles.
- Find the magnitude and direction of the velocity at a given time or position.
- Find the range on a horizontal plane and the greatest height achieved.
- Derive and use the cartesian equation of the trajectory of a projectile.