- Structure of Mathematical Proof
- Logical Connectives
- Disproof by Counter Example
- Proof by Deduction
- Proof by Exhaustion
- Proof by Contradiction
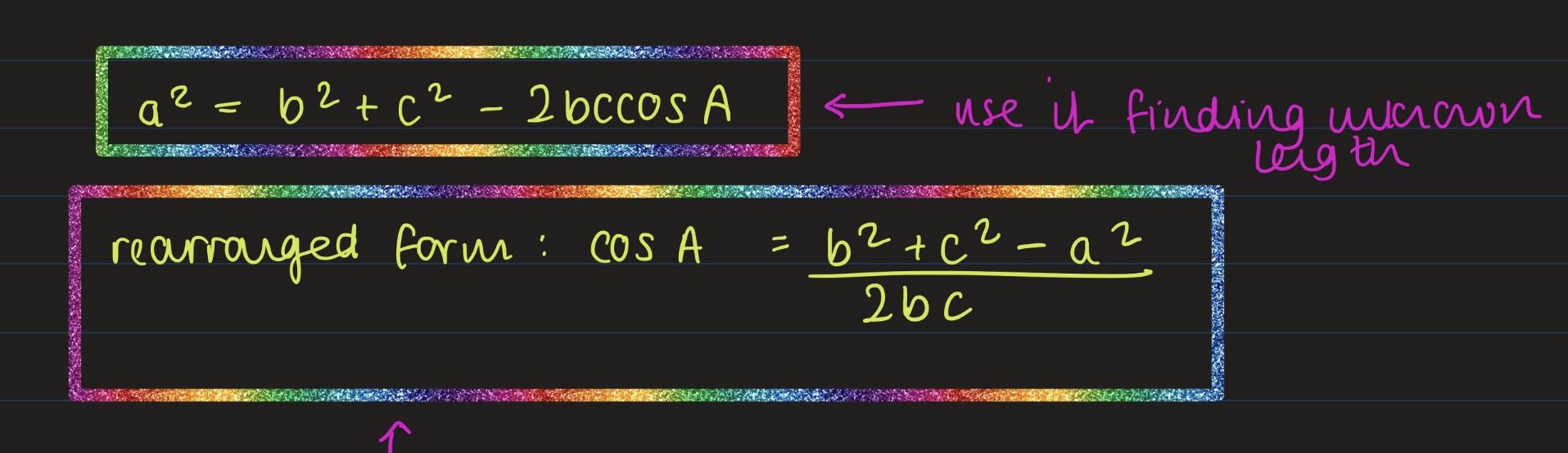
A-level Mathematics (Pure)
Full Revision Notes
(OCR A Syllabus)
Proof
Algebra and Functions
GCSE Recap
- Indices
- Surds
- Simultaneous Equations
- Quadratic Functions
- Inequalities
- Polynomials
The Modulus Function
- Understand and Use the Modulus Function
- Solve Equations and Inequalities involving the Modulus
- Solve Equations and Inequalities involving the Modulus Graphically
- Sketch the Modulus and the Modulus of Linear Functions
Functions
- Understand and be able to use the definiton of a function
- Vocabulary and associated notation i.e. many-one, one-many, one-one, mapping, image, range, domain
- Definitions of range and domain
- Understand and be able to use inverse functions and their graphs
- Know the conditions for the inverse function to exist
- Be able to find the inverse of a function either graphically, by reflection in the line y = x, or algebraically
- Composite functions
Graph Transformations
Partial Fractions
- Decompose rational functions into partial fractions
- Denominator will be up to squared terms and maximum three terms
- Numerator will be numerial or linear
- Use of factor theorem and polynomial division to form rational functions
- For Integration see later
Coordinate Geometry
Straight Lines Summary
- Equations of Straight lines
- Draw graphs of straight lines
- Find the midpoint of a line segment
- Find the distance between two points
- Find the intersection of two lines
- Gradient conditions of parallel and perpendicular lines
- Use straight line models in a variety of contexts
Circles
- Understand and be able to use the coordinate geometry of a circle including using the equation of a circle
- Be able to draw a circle given its euation or form the equation given its centre and radius
- Be able to complete the square to find the centre and radius of a circle
- Be able to investigate wheter a line and a circle or two circles intersect
- Circle Theorems
Parametric Equations
- Understand and use parametric equations of curves
- Convert between cartesian and parametric forms
- Sketch simple parametric curves
- Use parametric curves in modelling in a variety of contexts
Calculus with Parametric Equations
- Be able to differentiate simple functions defined parametrically
- Find the gradient of a point on a curve and use to find the equations of tangents and normals, and solve associated problems
Sequences and Series
Binomial Expansion
- Understand and be able to use the binomial expansion for positive integers of n
- Coefficient notations
- Calculate binomial coefficents
- Relationship to Pascal's traingle
- Know that 0! = 1
- Understand and know the link to binomial probabilities (see probability section)
- Extend the binomal expansion for any rational n
- Write (a+bx)n as an(1 + bx⁄a)n
- Know when the expansion is valid
Arithmetic Sequences
- Be able to work with sequences given b a formula for the nth term and generated by a simple relation
- Generate terms, find the nth term and comment on the mathematical behaviour of the sequence
- Understand the meaning of and work with increasing, decreasing and periodic sequences
- Know the difference between and be able to recognise a sequence and a series
- Know the difference between and be able to recognise finite and infinite series
- Understand and be able to use sigma notation
- Understand and be able to work with arithmetic sequences + series including the formula for the nth term and sum to n terms
Geometric Sequences
Modelling
Trigonometry
Definitions and Introduction
- Understand and use definitions for sin x, cos x and tan x
- Understand the functions, their graphs, symmetries and periodicities
- Know and use exact values of sin x, cos x, tan x for x = 0, 30, 45, 60, 90 (not for tan), 180 degrees and multiples thereof
- Know and be able to use simple trigonometric identities
- Be able to solve trigonometric equations in a given interval including quadratic equations in sin x, cos x and tan x and equations involving multiples of the known angle
Triangle Geometry
- Understand and use the sine and cosine rules
- Understand and be able to use the area of a triangle
Radians
- Be able to work with radian measure
- Use the relationship between degrees and radians
- Know and able to use exact values of sin x, cos x, tan x (table in notes)
- Extend knowledge of trigonmetric equations and identities to include radians
- Be able to work with radian measure and use for arc length and sector
Inverse Functions
- Understand and use definitions of arcsin x, arccos x and arctan x and their relationship to sin x, cos x and tan x respectively
- Know their graphs and relate them to the graphs of sin x, cos x and tan x
Modelling
- Be able to use trigonometric functions to solve problems in context
a cos x + b sin x
Small Angle Approximations
- Understand and be able to use the standard small angle approximations
Compound & Double Angle Formulae
- Understand and be able to use the double angle formulae and compound angle formulae
- Understand the geometric proofs of these formulae
- Be able to prove the double angle formulae
- Be able to construct proofs involving trigonometric functions and identities
- Use the formulae to solve trigonometric equations, prove identities or evaluate integrals
Reciprocal Functions
- Understand and be able to use the definitions of secant (sec x), cosecant (cosec x) and contangent (cot x)
- Understand and be able to use their relationship with sin x, cos x and tan x
- Understand the graphs of the functions, their ranges and domains
- Understand and be able to use the identities (see notes)
- Use the identities to solve trigonometric equations, prove identities or evaluate integrals
Exponentials and Logarithms
Differentiation
Integration
Indefinite Integration
- Know and be able to use the fundamental theorem of calculus
- Understand and be able to use the terms indefinite and definite when applied to integrals
- Be able to integrate xn (except n = -1) and related sums, differences and multiples
- Solve problems including evaluating a constant of integration
Definite Integration and Complex Functions
- Be able to integrate ekx,1⁄x, sin kx, cos kx, and related sums, differences and constant multiples
- Integrals of arcsin, arccos and arctan will be given if required
- This includes using trigonmetric relations (eg double angle formulae) to integrate functions such as cos2x
- Be able to evaluate definite integrals
- Be able to use a definite integral to find the area between a curve and x-axis
Partial Fractions and Integration
- Be able to integrate functions using partial fractions that have linear terms in their denominator
Complicated Areas
Integration as the limit of a sum
Integration by Substitution
Integration by Parts
Separable Differential Equations
Numerical Methods
Vectors
Vectors in 2D
- Be able to use vectors in two dimensions
- Column vectors and i,j notation
- Difference between a scalar and vector and distinguish between them when writing
- Calculate magnitude and direction of a vector
- Convert between magnitude/direction form and component form
- Calculate the modulus of a vector and interpret as magnitude
- Be able to add vectors diagrammatically
- Perform vector addition
- Multiply vectors by scalars
- Understand and be able to use position vectors
- Understand the meaning of displacement vector, component vector, resultant vector, parallel vector, equal vector and unit vector
- Calculate the distance between two points represented by position vectors
- Use vectors to solve problems in pure mathematics and in context, including forces (see forces notes)
- Use vectors to solve problems in kinematics (see kinematics notes)
Vectors in 3D
- Be able to use vectors in three dimensions
- Column vectors and i,j notation
- Extend points above to 3D (excluding the direction of a 3D vector)
